
目次
はじめに
普段、物事を考える際に帰納法や演繹法を意識して考えることは少ないかと思います。また帰納法や演繹法という言葉は知っていても違いが分からないということも多いのではないでしょうか。今回は、MBAで学ぶ思考術ということで、帰納法と演繹法、さらにはアブダクションについて簡単に説明したいと思います。帰納法と演繹法は、論理的推論の2つの主要な方法です。以下のようにそれぞれの特徴と違いをまとめます。
帰納法 (Inductive reasoning)とは
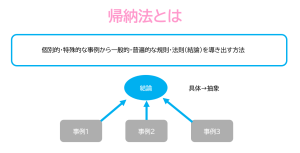
個別的・特殊的な事例から一般的・普遍的な規則や法則を導き出す方法です。
具体的な観察や事実から始まり、パターンを見つけ、一般化して理論を構築します。
結論は確実ではなく、確率的または蓋然的なものになります。
帰納法は新しい情報や理論を生み出すのに適しており、科学的研究、特に質的研究でよく使用されます。
演繹法 (Deductive reasoning)とは
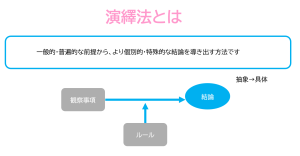
演繹法は一般的・普遍的な前提から、より個別的・特殊的な結論を導き出す方法です。
既知の一般的な理論や法則から始まり、特定の事例や結論を導き出します。
前提が真であれば、結論も必然的に真となります。既存の理論をテストしたり、特定の事例に適用したりするのに適しています。
数学や論理学でよく使用され、科学的研究、特に量的研究でも重要です。
帰納法と演繹法の主な違い
アプローチ方法の違い:
帰納法は「ボトムアップ」、演繹法は「トップダウン」のアプローチを取ります。
帰納法は「たくさんの例から、全体のルールを見つける」方法です。
帰納法の例
– あなたが毎日空を見ていて、「太陽は朝に東から昇って、夕方に西に沈む」と気づきました。
– これを何日も何日も見ていると、「太陽はいつもこうなんだ」というルールを発見します。
これが帰納法です。たくさんの観察(具体)から、大きなルール(抽象)を作り出すのです。
演繹法は「すでにわかっているルールから、新しいことを見つける」方法です。
演繹法の例
– 「すべての哺乳類は体温が一定である」というルールを知っています。
– 「犬は哺乳類である」ということも知っています。
– だから、「犬の体温は一定である」という新しいことがわかります。
これが演繹法です。知っているルールを使って、新しい事実を導き出すのです。
簡単にまとめると:
– 帰納法: たくさんの小さな例 →大きなルール
– 演繹法: 大きなルール → 新しい事実
になります。
実際の研究や問題解決では、両方の方法を組み合わせて使用することが多く、それぞれの長所を活かすことが重要です
アブダクション(仮説形成)
似たような考えに、アブダクション(仮説形成)があります。アブダクション(abduction)は、演繹法や帰納法とは異なる第三の推論形式として知られています。
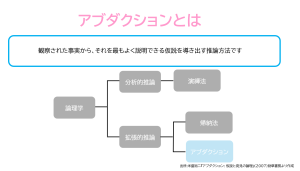
アブダクションと帰納法には以下のような主な違いがあります。
1. 推論の方向性:
– 帰納法は個別の事例から一般的な結論を導き出す「下から上へ」の推論です。
– アブダクションは観察された現象に対して最も説得力のある説明を推測する「横向き」の推論です。つまり、結果から原因を推測し、最も説得力のある仮説を形成するのに用いられます。
2. 結論の性質:
– 帰納法の結論は一般化された法則や規則性を示します。
– アブダクションの結論は特定の現象に対する最も妥当な説明や仮説を提示します。
3. 確実性:
– 帰納法の結論は確率的で、必ずしも真とは限りません。
– アブダクションの結論はさらに不確実で、最も可能性が高い説明を提示するに留まります。
4. 目的:
– 帰納法は一般的な法則や理論の構築を目指します。
– アブダクションは特定の現象の説明や原因の推測(仮説形成)を目的とします。
5. 適用場面:
– 帰納法は多くの事例から共通点を見出す場合に適しています。
– アブダクションは限られた情報から最善の説明を導く必要がある場合に有効です。
アブダクションの例
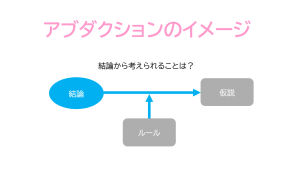
アブダクションの簡単な例としては、
– 道路が濡れている。雨が降ると道路が濡れる。きっと雨が降ったに違いない。
というようにまず結論があってそれを構成するための仮説を考えるプロセスになります。
これは、ビジネスに置き換えてみると、上司にどうして売り上げが急に上がったのか調べて欲しいという依頼があり、それに対する仮説を考えるシーンを想像してみればイメージしやすいのではないのでしょうか。
注意すべき点は、アブダクションによって導かれた仮説は、必ずしも正しいとは限りません。検証を行ったり、他の推論方法との組み合わせが大切です。アブダクションは、特に不確実性の高い状況や新しい分野での問題解決において有用な思考法だと言われています。ただし、その性質上、導き出された仮説の妥当性を慎重に検討する必要があります。
